統計入門！回帰分析の基本を学ぼう！ - 双子ママ、今日も楽しい！

先日、t検定について復習した記事を書きましたが、今回はその続きで 「回帰分析」 のお話です。

（t検定の記事も、よかったら読んでみてくださいね♪）

わかったつもり、になりがちだからこそ…

いろんなことを学ぶと、「なるほど、わかった！」って思いがち。でも、自分の言葉で説明しようとすると、意外と言葉が出てこない…。 そんな経験ありませんか？

私もまさにそれで、「これはまだちゃんと理解できてないな」と感じることがあります。

だからこそ、自分だけがわかればいいメモ ではなく、誰かに読んでもらっても伝わるような言葉でまとめてみよう！ と思って書いています。

簡単に言うと、

1つまたは複数の「理由（＝変数）」から、「結果（＝変数）」を予測する分析方法です。

たとえば、「テストの点数」という結果が、「勉強時間」や「睡眠時間」などの理由で決まっているとしたら、それを数式にして表せるようにするのが回帰分析です。

→ 独立変数が1つ の回帰分析

→ 独立変数が複数 の回帰分析

回帰分析では、独立変数（理由）と従属変数（結果）との関係を見つけて、数式にまとめていきます。

たとえば…

「1時間勉強すると、テストの得点が10点上がるらしいぞ…？」

というルールを見つけるような感じです。

これを数式で書くと：

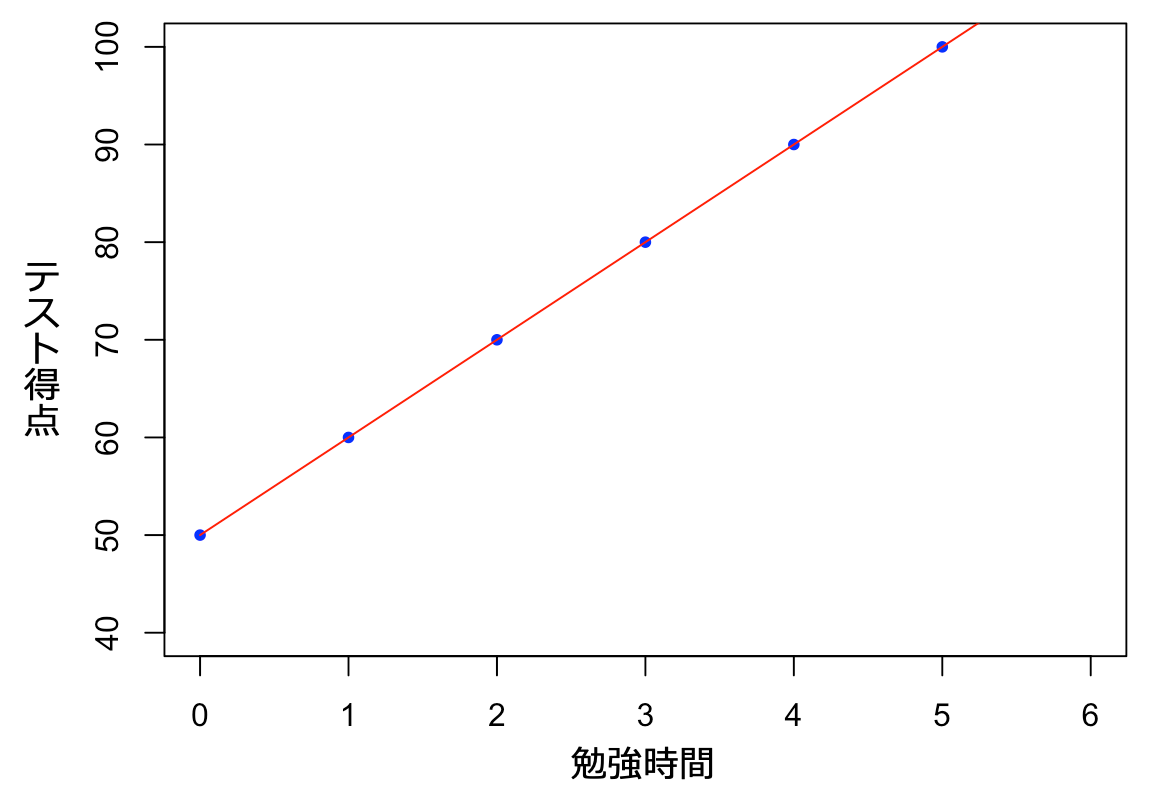
テスト得点 ＝ 50点 ＋ 10点 × 勉強時間（時間）

この関係を グラフ にすると、真っ直ぐな線（回帰直線）が引けます。

この回帰直線がどれだけ「当てはまっているか」や「信頼できるか」を調べるために使うのが、以下の指標です。

→ 予測（モデル）がどれくらいデータをうまく説明できているかの指標

→ 0〜1の間の値で、1に近いほどピッタリ！

→ その関係がたまたまじゃなく、本当に意味があるかどうか

→ 小さいほど（たとえば0.05未満）信頼できる関係だと言えます。

用語	説明
従属変数（目的変数）	予測したい結果（例：テスト点数）
独立変数（説明変数）	原因・理由となる変数（例：勉強時間）
回帰式	変数間の関係を表す式（例：点数＝5×時間＋30）
切片	独立変数が0のときの目的変数の値（30）
回帰係数（傾き）	独立変数が1増えると目的変数がどれくらい増えるか（5）
単回帰分析	独立変数が1つの場合の分析
重回帰分析	独立変数が複数ある場合の分析
残差	実際の値と予測値との差
決定係数 R²	どのくらいモデルがデータをうまく説明できているか（1に近いほど良い）
p値	偶然かどうかの指標（0に近いほど関係が確か）