前回のおさらい
前回の記事では、統計モデリングを進めるには、「確率分布」の理解がとても大事だということがわかりました。
(まだ読んでいない方は、ぜひ前回の記事も読んでみてくださいね)
「確率分布」とは、データが従うと仮定されるパターンのこと。
そしてその分布の“形”や“広がり”を決めるのが「パラメーター」でした。
分布によって、持つパラメーターが違うんですよね。
なんでも正規分布…じゃない?
これまで私は、どんなデータもとりあえず「正規分布」と仮定して分析していました。
でも実は、データの性質によって、適した分布は違うんです。
今回は、代表的な確率分布とそのパラメーターをまとめてみました。
確率分布とパラメーターの関係
確率分布は、「値がどのくらいの確率で現れるか?」を示すルールです。
パラメーターは、その分布の「形」や「位置」、「広がり」を決める数値。
つまり、分布の形はパラメーターによって決まるということです。
主な確率分布とパラメーター
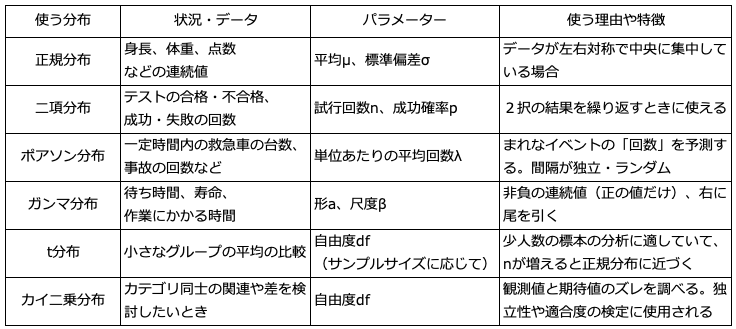
正規分布(Normal distribution)
-
使うデータ:連続値で、左右対称にばらつくデータ
-
パラメーター:
-
平均 μ(山の中心)
-
標準偏差 σ(広がりの大きさ)
-
-
例:身長、体重、テストの点数、IQなど
-
特徴:「釣鐘型」の形。多くのデータが「平均 ± 標準偏差」に集まる。
たとえば:
μ = 160, σ = 5 → 「多くの人は155〜165cm」
μ = 160, σ = 20 → 「140〜180cmとばらつきが大きい」
二項分布(Binomial distribution)
-
使うデータ:「成功 or 失敗」など2択の結果をn回くり返す
-
パラメーター:
-
試行回数 n
-
成功確率 p
-
-
例:10回コインを投げて表が出た回数
-
特徴:各試行が独立で、pが一定
たとえば:
n = 10(10回投げる)、p = 0.5(表が出る確率)
→ 「表が7回出る確率」を求めたいときに使える
ポアソン分布(Poisson distribution)
-
使うデータ:「一定時間・空間内での発生回数」
-
パラメーター:λ(単位あたりの平均発生回数)
-
例:1時間に来る救急車の台数
-
特徴:まれに起こるイベントを扱うのに向いている
たとえば:
λ = 3(平均して1時間に3件)
→ 「ある1時間に何件来るか?」を予測できる
ポアソン分布が使える条件:
-
イベントの発生がランダム
-
イベント間が独立している
ガンマ分布(Gamma distribution)
-
使うデータ:0以上の連続値で、右に裾が長い分布
-
パラメーター:形 α(alpha)、尺度 β(beta)
-
例:作業時間、寿命、待ち時間など
-
特徴:指数分布の一般化。いろんな形に柔軟に対応できる
t分布(t-distribution)
-
使うデータ:少人数のデータで平均を比較したいとき
-
パラメーター:自由度 df(データ数により変化)
-
例:10人 vs 10人のグループで平均の差を見る
-
特徴:サンプルサイズが小さいときに使い、nが大きくなると正規分布に近づく
カイ二乗分布(Chi-square distribution)
-
使うデータ:カテゴリデータの「差の検定」や「分散の分析」など
-
パラメーター:自由度 df
-
例:「期待通りの割合と違っていたか?」を検定(適合度検定や独立性の検定)
こんな時はこの確率分布!一覧表
私はどの分布を使う?
ちなみに、私が今分析してみようと思っているのは、「反応時間」のデータです。
よく考えてみると、反応時間ってマイナスになることはないですよね。そして、連続的な値として測れるので、「ガンマ分布」が合いそうだな〜と思っています。
一方で、これまでよく分析していたP300(背景脳波を加算して出す、事象関連電位)は、平均を取ると正規分布に近づきやすいので、「正規分布」でよさそうです。
つまり、同じ人から同時に取れたデータでも、種類によって仮定する分布が違うんですね。
ちょっとややこしいけど…そこがまた、分析の面白いところでもあります!

まとめ
統計モデリングをするには…
-
どの分布を使うか?
-
その分布にはどんなパラメーターがあるか?
をきちんと理解して選ぶことがとても大切です!
(私は、まだ全てが頭に入っていないので、時々このページを見て、確認しちゃいます!笑)

